Hamiltonian

The Hamiltonian here is simply a cropped coupling of the Non-adiabatic couplings plus the external field.

The total Hamiltonian of namd_lmi consists of three parts: \begin{equation} \mathcal{H} = \mathcal{H}^0 + \mathcal{H}^{NAC} + \mathcal{H}^{LMI} \end{equation} where \(\mathcal{H}^0\) is just eigenvalues of KS orbitals and \(\mathcal{H}^{NAC}_{jk} = -i\hbar \mathbf{D}_{jk}\) models the e-ph and spin-orbit coupling (if LSORBIT=.TRUE. is used). The LMI term reads \(\mathcal{H}_{jk}^{\mathrm{LMI}} = -e \frac{\mathbf{A}}{m_e} \mel{j}{\mathbf{p}}{k}\). The vector potential term \(\mathbf{A}\) is calculated by integrating the external electric field \begin{equation} \mathbf{A}(t) = - \int_0^t \mathbf{E}(t') \dd t' \end{equation}

Help message

$ namd_lmi hamil --help
Generate the Hamiltonian from NAC according to config file

Usage: namd_lmi hamil [OPTIONS]

Options:
  -c, --config <CONFIG>
          Config file name.

          Aliases: "cfg", "conf".

          [default: hamil_config.toml]

      --generate <GENERATE>
          Generate auxiliary files for the calculation and analysis.

          The generation of Hamiltonian will not run if this flag is set.

          Alias: "gen".

          Possible values:
          - config-template:      Generate config template for Hamiltonian generation. Aliases: "config", "cfg" and "conf"
          - efield-template:      Generate script template for external electric field. Aliases: "efield", "ef"
          - postprocess-template: Generate post-process scripts for Hamiltonian analysis. Aliases: "post-process", "postprocess", "pp"

  -h, --help
          Print help (see a summary with '-h')

Procedures

Generate a configuration template, and an optical field description file

$ namd_lmi hamil --generate conf
2024-11-19 21:49:48 [ INFO] Global logger initialized with targets being stderr and "./globalrun.log"
2024-11-19 21:49:48 [ INFO] Writing `02_hamil_config_template.toml` ...
2024-11-19 21:49:48 [ INFO] Writing config to file "02_hamil_config_template.toml"
2024-11-19 21:49:48 [ INFO] Time used: 1.624654ms

$ namd_lmi hamil --generate efield
2024-11-20 11:34:14 [ INFO] Global logger initialized with targets being stderr and "./globalrun.log"
2024-11-20 11:34:14 [ INFO] Writing `efield_template.rhai` ...
2024-11-20 11:34:14 [ INFO] Time used: 977.069µs

Modify the Hamiltonian configuration file and optical description file

Hamiltonian configuration

The file 02_hamil_config.toml should read
```
# NAMD-lmi config for Hamiltonian generation

      ikpoint = 1
   basis_list = "215..220"
 basis_labels = ["VBM-1", "VBM", "CBM", "CBM+1", "CBM+2", "CBM+3"]
    nac_fname = "NAC.h5"
 efield_fname = "./efield.rhai"
  hamil_fname = "HAMIL.h5"
   propmethod = "Expm"
      scissor = 1.5 # unit: eV
```
Explanation of each field:
- ikpoint integer: K point index, consistent with NAC's configuration.
- basis_list string: THIS FIELD SHOULD BE A STRING., list of bands to form the basis.
  - Positive one indicates the spin-up band;
  - Negative one indicates the spin-down band.
  - Zeros are not allowed
  You can specify a consecutive bands with multiple ranges or singletons:
  
  A range is a pattern of start..end where
```
- start and end are integers with same sign (both + or both -)
- |start| <= |end|
- no other characters (whitespace or any other thinds) around `..`
```
  And multiple ranges and singletons are separated with one or more whitespaces.
  
  EXAMPLE:
```
- `1..4` expands to `[1, 2, 3, 4]`;
- `1..1` expands to `[1]`;
- `4..1` expands to empty list `[]`;

- `-1..-4` expands to `[-1, -2, -3, -4]`.
- `-4..-4` expands to `[-4]`
- `-4..-1` expands to empty list `[]`;

- Tokens like `-4..4` `1 ..3`, `0`, `-3..0`, `-3..3` are not allowed.
```
  "-1..-4 1..4" expands to [-1, -2, -3, -4, 1, ,2 , 3, 4], and meaning that band 1 to 4 with spin down and band 1 to 4 with spin up form the total basis.
- basis_labels list of strings: Labels of each band in the basis. This field is optional, or it must have the same length with expanded basis_list.
- nac_fname string: File name of the pre-calculated NAC by last procedure (namd_lmi nac -c config).
- efield_fname string: Name of the optical field description file. If no optical field is applied, this field can be commented out.
- hamil_fname string: File name of output Hamiltonian.
- propmethod string: Numerical method to solve of time-dependent Schrodinger equation (TDSE). Here are supported methods:
  - Expm: Matrix exponentiation by Padé approximant.
  - Exact: Matrix power by diagonalization.
  - FiniteDifference/FD: Solve TDSE using finite difference method. This method usually requires fine time steps in the next step.
  - LiouvilleTrotter/LT: Using Trotter formula to solve TDSE, proposed by Akimov, A. V., & Prezhdo, O. V. J. Chem. Theory Comput. 2014, 10, 2, 789–804
  It should be noted that Expm, Exact are usually slow while they have large tolerance of time step, resulting in much higher performance beyond FiniteDifference. Large time step also can be used with LiouvilleTrotter method, while it requires the off-diagonal elements of Hamiltonian to be real, which are usually not viable for photo-excitation processes.
- scissor float: Scissor opeartor for the gap correction. The photo-excitation process requires a high-precision time-averaged band gap over AIMD, and this parameter can modify the gap to target value.

Optical field description

The efield_template.rhai should read like

//
// Example rhai script for ELECTRIC FIELD input
//
// This script uses `rhai` as the scripting language.
//
// For detailed usage of `rhai`, please see https://rhai.rs/book and turn to
// chapter "Scripting Language".
//
//
// Available operators:
//      +   +=
//      -   -=
//      *   *=
//      /   /=
//      %   %=      (modulo operator)
//      **  **=     (power operator, `a ** b` equals `a` raised to the `b` power)
//      ==  !=
//      <   <=
//      >   >=
//      ..  ..=     ( .. is exclusive range, ..= is inclusive range )
//                  example: (1 .. 9) == (1 ..= 8)
//
//      Detailed help: https://rhai.rs/book/language/num-op.html
//
// Pre-defined constants:
//
//      - e: Euler's number, aka the base of natural logarithms
//      - pi: π
//
// Pre-defined mathematical functions:
//
//      - trigonometric:
//          sin     cos     tan
//          sinh    cosh    tanh
//          asin    acos    atan
//          asinh   acosh   atanh
//
//      - numerical:
//          sqrt(x)
//          exp(x) (base of E)
//          ln(x) (base of E)
//          log(x) (base of 10), or log(x, base)
//
//      - rounding:
//          floor
//          ceiling
//          round
//          int
//          fraction
//
//      - conversion:
//          to_degrees
//          to_radians
//
//      - comparison:
//          min
//          max
//
//
// You must define a function named `efield` with only one parameter typed with float64.
//
// And this function must return an array with exactly 3 float64 elements.
//
// This function will be evaluated from `t=0.0` to `t=namdtime*potim` (exclusive)
//
fn efield(t) {
    let hbar  = 0.658212;           // reduced planck constant (eV/fs)
    let amp   = 0.005;              // amplitude = 0.005 (Volt/Angstrom)
    let hnu   = 1.4;                // photon energy = h * nu = 1.4 (eV)
    let omega = hnu / hbar;         // omega = hnu / hbar (rad/fs)

    let x = amp * cos(omega * t);   // electric field at `x` direction at time `t`
    let y = amp * sin(omega * t);   // electric field at `y` direction at time `t`
    let z = 0.0;                    // no electric field at `z` direction

    return [x, y, z];               // this statement is required.
}

where the contents after with // are just comments for rhai syntax illustration.

This file describes an persistent uniform \(\sigma^+\) optical field, with \(h\nu = 1.4 \mathrm{eV}\), amplitude \(A_0 = 0.005 \mathrm{V/Angstrom}\).

If you want to impose an optical pulse, an envelop function should be used before return [x, y, z].

For example, a Gaussian pulse:

fn efield(t) {
    let hbar  = 0.658212;           // reduced planck constant (eV/fs)
    let amp   = 0.005;              // amplitude = 0.005 (Volt/Angstrom)
    let hnu   = 1.4;                // photon energy = h * nu = 1.4 (eV)
    let omega = hnu / hbar;         // omega = hnu / hbar (rad/fs)

    let x = amp * cos(omega * t);   // electric field at `x` direction at time `t`
    let y = amp * sin(omega * t);   // electric field at `y` direction at time `t`
    let z = 0.0;                    // no electric field at `z` direction

    let sigma = 1000.0;             // sigma of gaussian function, in femto second
    let mu    = 1000.0;             // center of the pulse, in femto second
    let envelop = exp(-(t-mu)**2 / sigma**2 / 2.0);

    return [x * envelop, y * envelop, z * envelop];
}

a sine pulse:

fn efield(t) {
    let hbar  = 0.658212;           // reduced planck constant (eV/fs)
    let amp   = 0.005;              // amplitude = 0.005 (Volt/Angstrom)
    let hnu   = 1.4;                // photon energy = h * nu = 1.4 (eV)
    let omega = hnu / hbar;         // omega = hnu / hbar (rad/fs)

    let x = amp * cos(omega * t);   // electric field at `x` direction at time `t`
    let y = amp * sin(omega * t);   // electric field at `y` direction at time `t`
    let z = 0.0;                    // no electric field at `z` direction

    let duration = 1000.0;          // Pulse duration, 1000 fs
    let omega_envelop = 2.0 / duration * pi;    // Envelop angular frequency

    let envelop = if t <= duration {
        sin(omega_envelop*t - 0.5*pi) * 0.5 + 0.5;
    } else {
        0.0
    };

    return [x*envelop, y*envelop, z*envelop];   // this statement is required.
}

Generate Hamiltonian

$ namd_lmi hamil -c 02_hamil_config_template.toml
2024-11-25 11:15:53 [ INFO] Global logger initialized with targets being stderr and "./globalrun.log"
2024-11-25 11:15:53 [ INFO]
+----------------------------------------------------------------------+
|                                                                      |
|    _   _            __  __  _____           _       __  __  _____    |
|   | \ | |    /\    |  \/  ||  __ \         | |     |  \/  ||_   _|   |
|   |  \| |   /  \   | \  / || |  | | ______ | |     | \  / |  | |     |
|   | . ` |  / /\ \  | |\/| || |  | ||______|| |     | |\/| |  | |     |
|   | |\  | / ____ \ | |  | || |__| |        | |____ | |  | | _| |_    |
|   |_| \_|/_/    \_\|_|  |_||_____/         |______||_|  |_||_____|   |
|                                                                      |
+----------------------------------------------------------------------+

Welcome to use namd!
    current version:    0.1.0
    git hash:           NO GIT INFO
    author(s):          Ionizing
    host:               x86_64-unknown-linux-gnu
    built time:         2024-11-21 11:27:32 +08:00

2024-11-25 11:15:53 [ WARN] Field 'hamil_fname' points to an existing file and it will be overwritten.
2024-11-25 11:15:53 [ INFO] Got Hamiltonnian config:
# NAMD-lmi config for Hamiltonian generation

              ikpoint = 1
           basis_list = [215, 216, 217, 218, 219, 220]
         basis_labels = ["VBM-1", "VBM", "CBM", "CBM+1", "CBM+2", "CBM+3"]
            nac_fname = "NAC.h5"
         efield_fname = "./efield.rhai"
          hamil_fname = "HAMIL.h5"
           propmethod = "Expm"
              scissor = 1.5

2024-11-25 11:15:53 [ INFO] Got electric field from file "./efield.rhai" with content of:
//
// Example rhai script for ELECTRIC FIELD input
//
...
...
    return [x, y, z];               // this statement is required.
}

2024-11-25 11:15:53 [ INFO] Found Efermi = -2.824 eV, shift band eigvals to align with it ...
2024-11-25 11:15:53 [ INFO] Found scissor opeartor of 1.5000 eV. current system has gap of 1.5156 .. 1.5303 .. 1.5457 (min .. avg .. max) (eV).
                     Now the gap is set to 1.4853 .. 1.5000 .. 1.5155 (min .. avg .. max) (eV). min(CBM_t) - max(VBM_t) =   1.4579
2024-11-25 11:15:53 [ INFO] Time used: 156.235792ms

Visualize the Hamiltonian

Run namd_lmi hamil --generate pp to get hamil_plot.py, and then run it to get .pngs

$ namd_lmi hamil --generate pp
2024-11-20 16:07:04 [ INFO] Global logger initialized with targets being stderr and "./globalrun.log"
2024-11-20 16:07:04 [ INFO] Writing `hamil_plot.py` ...
2024-11-20 16:07:04 [ INFO] Time used: 1.868109ms

$ python3 hamil_plot.py HAMIL.h5

Writing hamil_nac.png
Writing hamil_pij.png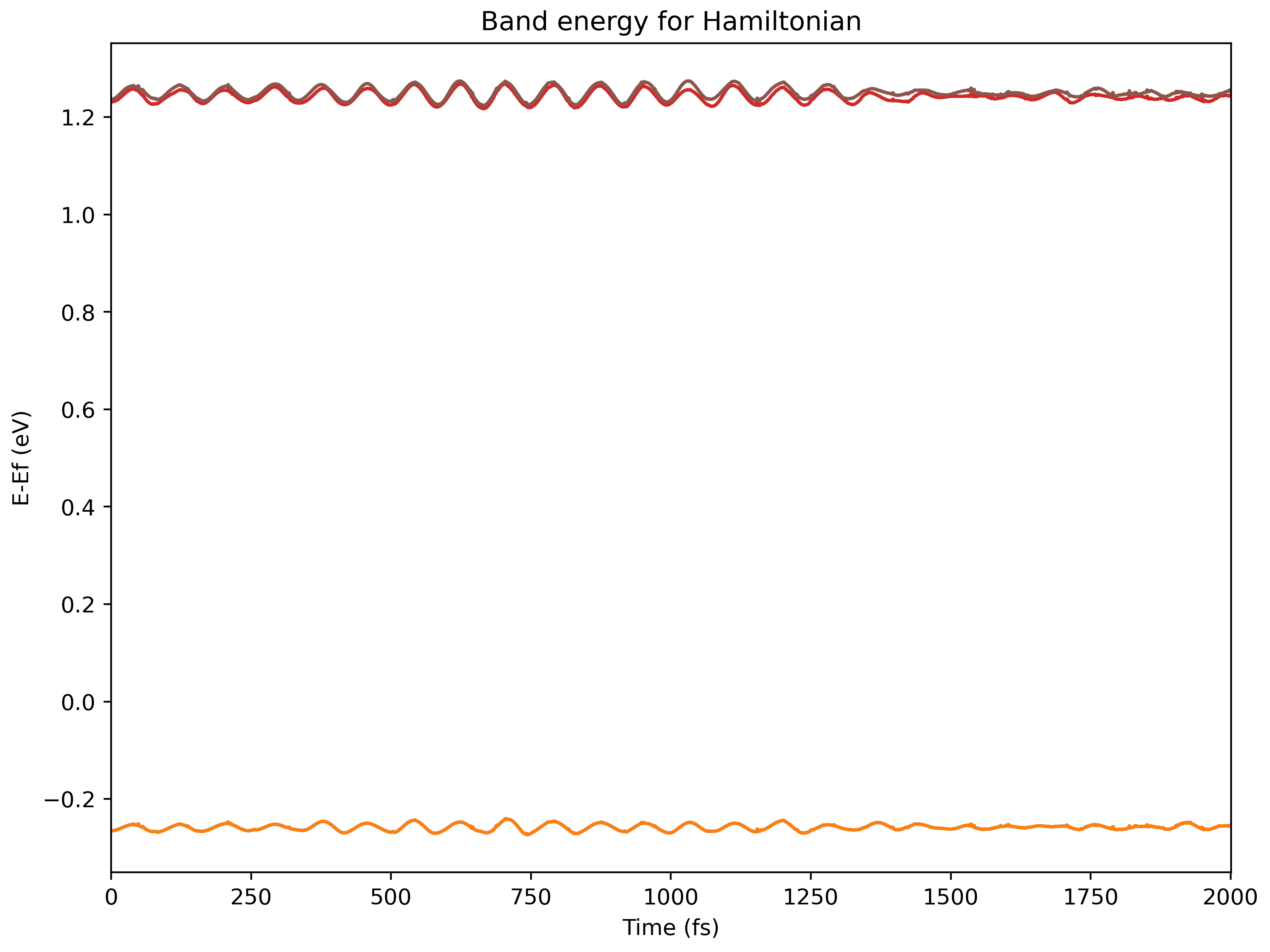

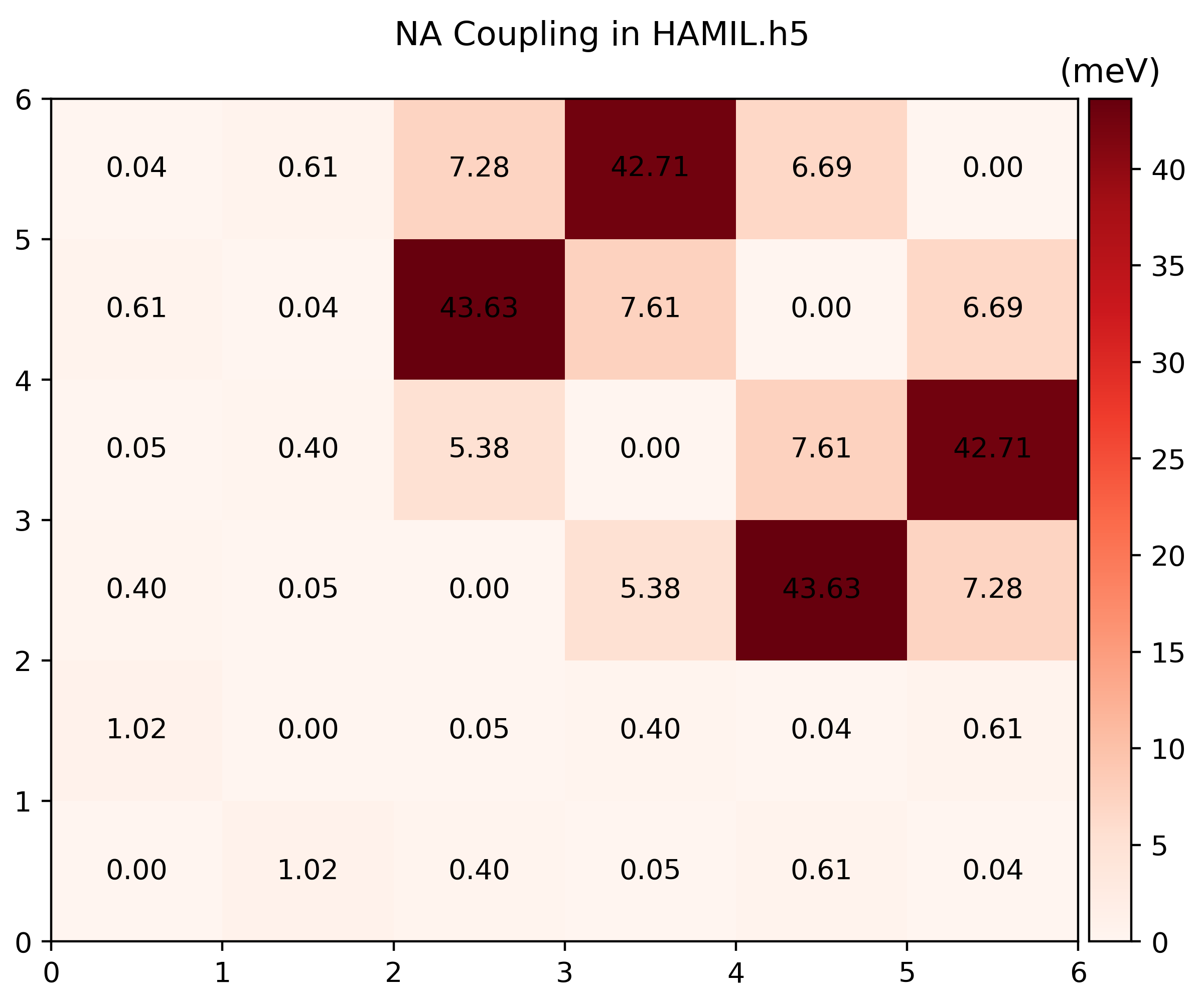
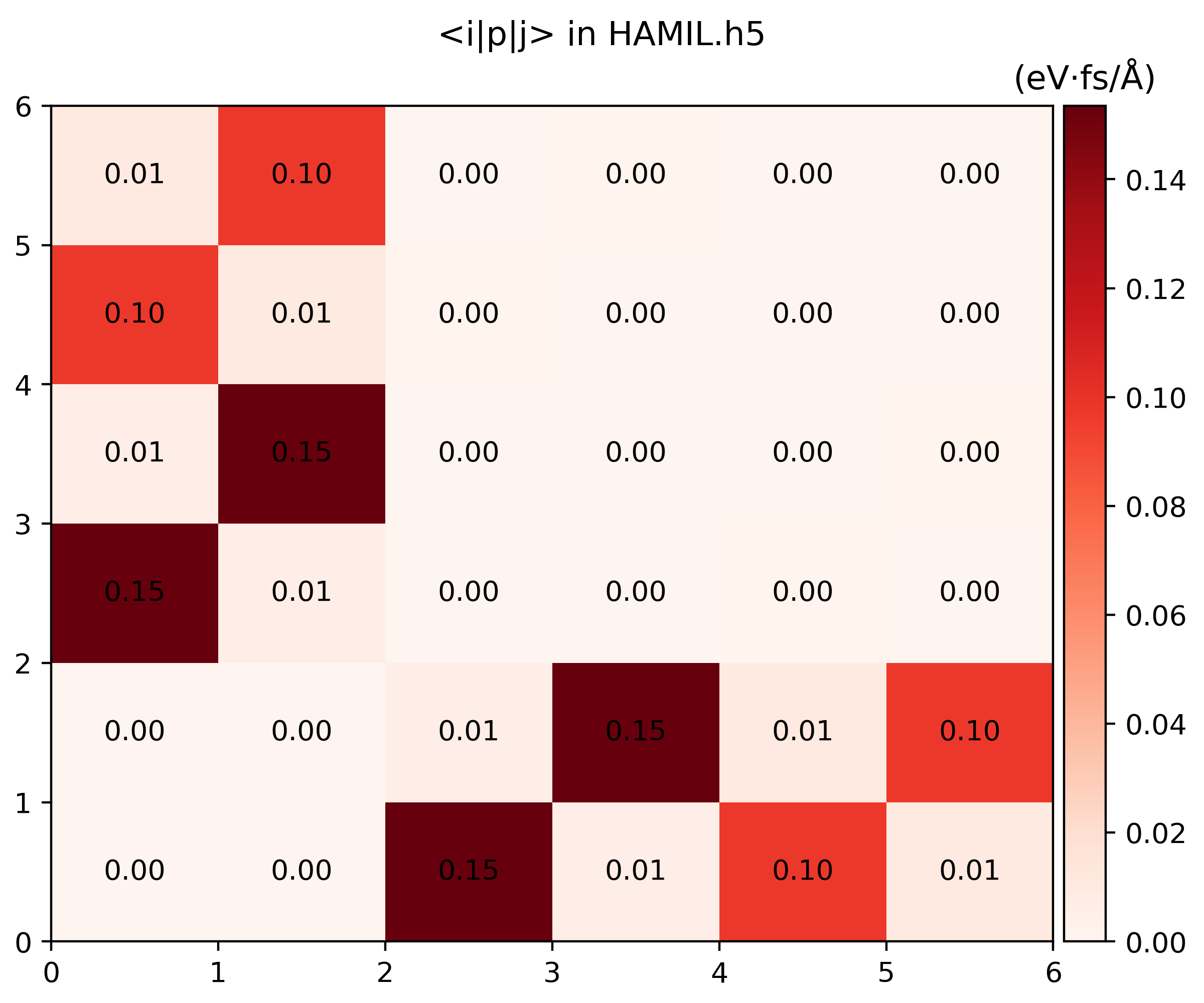
Bands inside Hamiltonian NAC inside Hamiltonian Momentum matrix elements Hamiltonian

Data fields of HAMIL.h5

HDF5 "HAMIL.h5" {
GROUP "/" {
   DATASET "basis_labels" {
      DATATYPE  H5T_STD_U8LE
      DATASPACE  SIMPLE { ( 31 ) / ( 31 ) }
   }
   DATASET "basis_list" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 6 ) / ( 6 ) }
   }
   DATASET "efield" {
      DATATYPE  H5T_STD_U8LE
      DATASPACE  SIMPLE { ( 2263 ) / ( 2263 ) }
   }
   DATASET "eig_t" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 1999, 6 ) / ( 1999, 6 ) }
   }
   DATASET "ikpoint" {
      DATATYPE  H5T_STD_U64LE
      DATASPACE  SCALAR
   }
   DATASET "nac_t_i" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 1999, 6, 6 ) / ( 1999, 6, 6 ) }
   }
   DATASET "nac_t_r" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 1999, 6, 6 ) / ( 1999, 6, 6 ) }
   }
   DATASET "nbasis" {
      DATATYPE  H5T_STD_U64LE
      DATASPACE  SCALAR
   }
   DATASET "ndigit" {
      DATATYPE  H5T_STD_U64LE
      DATASPACE  SCALAR
   }
   DATASET "nsw" {
      DATATYPE  H5T_STD_U64LE
      DATASPACE  SCALAR
   }
   DATASET "pij_t_i" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 1999, 3, 6, 6 ) / ( 1999, 3, 6, 6 ) }
   }
   DATASET "pij_t_r" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 1999, 3, 6, 6 ) / ( 1999, 3, 6, 6 ) }
   }
   DATASET "potim" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SCALAR
   }
   DATASET "proj_t" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 1999, 6, 36, 9 ) / ( 1999, 6, 36, 9 ) }
   }
   DATASET "propmethod" {
      DATATYPE  H5T_STD_U8LE
      DATASPACE  SIMPLE { ( 4 ) / ( 4 ) }
   }
   DATASET "scissor" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SCALAR
   }
   DATASET "temperature" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SCALAR
   }
}
}

NAMD-LMI Manual

Hamiltonian

Help message

Procedures